 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
二维连续型随机向量(X,Y)的联合概率密度为试确定A的值并求(X,Y)的联合分布函数。
二维连续型随机向量(X,Y)的联合概率密度为
试确定A的值并求(X,Y)的联合分布函数。
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
二维连续型随机向量(X,Y)的联合概率密度为
试确定A的值并求(X,Y)的联合分布函数。
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案
 更多“二维连续型随机向量(X,Y)的联合概率密度为试确定A的值并求…”相关的问题
更多“二维连续型随机向量(X,Y)的联合概率密度为试确定A的值并求…”相关的问题
设随机向量(X,Y)的概率密度为:
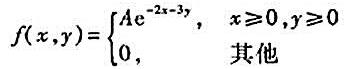
(1)确定常数A的值;
(2)求关于X和关于Y的边缘密度,并判定其独立性;
(3)计算P{0≤X≤1/2,0≤Y≤1/3}。
A.中间低两边高的凹型曲线
B.中间高两边低的凸型曲线
C.没有规律的随机曲线
D.近似直线段
A.中间低两边高的凹型曲线
B.中间高两边低的凸型曲线
C.没有规律的随机曲线
D.近似直线段
●试题八
阅读以下说明和C++代码,将解答写入答题纸的对应栏内。
【说明】
源程序文件vectorClass.cpp,其中定义了用于表示向量的类vector,但类vector的定义并不完整。请按要求完成下列操作,将类vector的定义补充完整,并给出输出结果。
1.补充类vector的构造函数,该函数有参数x和y,它们都是int型的数据,默认值都为0。请使用参数列表的形式分别将类的数据成员a和b分别初始化为参数x和y的值。
2.完成类vector的成员函数input(int x,int y)的定义,将int型的参数x和y分别赋值给数据成员b和a。
3.完成类vector的友元函数friend double Multiply(vector &x,vector &y)的定义,先定义double型的临时变量c,然后将参数对象x和对象y的数据成员a与b分别相乘再相加后赋值给c,最后返回c的值。
注意:除在指定位置添加语句之外,请不要改动程序中的其他内容。
源程序文件vectorClass.cpp清单如下:
#include <iostream.h>
class vector
{
int a;
int b;
public:
vector((1) ): (2)
{
}
void input(int x,int y)
{ (3)
}
void output()
{
cout<<'('<<a<<','<<b<<")"<<endl;
}
friend double Multiply(vector &x,vector &y);
};
double Multiply(vector &x,vector &y)
{
double c;
(4)
return c;
}
void main()
{
vector x(10,20),y;
double d;
y.input(2,3);
d=Multiply(x,y);
cout<<d<<endl;
}
程序输出结果是: (5) 。
某程序每获得一对随机数(x,y),都判断x2+y2≤1是否成立。如果N对随机数中,有m对满足这个不等式,则当N足够大时,数值m/N将会比较接近(57)。
A.必然有一半数小于1/2,有一半数大于1/2
B.大致顺序、等间隔地排列于(0,1)之间
C.其中落在任意子区间(a,b)中的数的比率大致接近于b-a
D.从小到大排序后,各个数都分别位于(0,1)的Ⅳ等分子区间内
A.保税集团
B.保税仓库
C.保税物流中心(A)型
D.保税物流中心(B)型
采用线性链表表示一个向量时,要求占用的存储空间地址()。
A.必须是连续的
B.部分地址必须是连续的
C.一定是不连续的
D.可连续可不连续
.jpg) 则冰箱品牌A与B在该地区最终将逐步稳定到市场占有率______。
则冰箱品牌A与B在该地区最终将逐步稳定到市场占有率______。A.(1/4,3/4)
B.(1/3,2/3)
C.(1/2,1/2)
D.(2/3,1/3)
设A是n*n常数矩阵(n>1),X是由未知数X1、X2、…、Xn组成的列向量,B是由常数b1、b2、…、bn组成的列向量,线性方程组AX=B有唯一解的充分必要条件不是______。
A.A的秩等于n
B.A的秩不等于0
C.A的行列式值不等于0
D.A存在逆矩阵