题目内容
（请给出正确答案）
[主观题]
欧氏空间V中的线性变换称为反称的，如果对任意，α，β∈V，证明：1)为反称的充分必要条件是，在一组标
欧氏空间V中的线性变换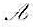
称为反称的，如果对任意，α，β∈V，
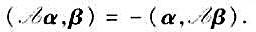证明：
1)
为反称的充分必要条件是，在一组标准正交基下的矩阵为反称的;
2)如果V1是反称线性变换的不变子空间，则
也是。
查看答案
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
欧氏空间V中的线性变换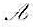称为反称的，如果对任意，α，β∈V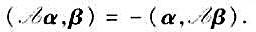，证明：
1)为反称的充分必要条件是，在一组标准正交基下的矩阵为反称的;
2)如果V1是反称线性变换的不变子空间，则也是。
如果结果不匹配，请 联系老师 获取答案
更多“欧氏空间V中的线性变换称为反称的，如果对任意，α，β∈V，证…”相关的问题
设V是复数域上的n维线性空间，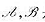
是V的线性变换，且
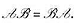证明：
1)如果λ0是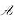
的一特征值，那么
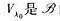的不变子空间;
2)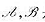至少有一个公共的特征向量。
1)设α，β是n维欧氏空间V中两个不同的单位向量，证明：存在一镜面反射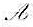
使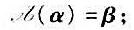
2)证明：n维欧氏空间V中任一正交变换都可以表成一系列镜面反射的乘积。
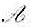是n维线性空间V上的线性变换，证明：
1)若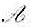在V的某基下矩阵A是某多项式d(λ)的友矩阵，则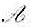的最小多项式是d(λ);
2)设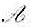的最高次的不变因子是d(λ)，则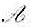的最小多项式是d(λ)。
设ε1，ε2，ε3，ε4四维线性空间V的一组基，已知线性变换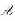
在这组基下的矩阵为
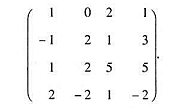
1)求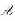在基
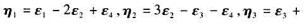
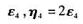下的矩阵;
2)求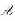的核与值域;
3)在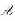的核中选一组基，把它扩充成V的一组基，并求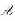在这组基下的矩阵;
4)在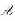的值域中选一组基，把它扩充成V的一组基，并求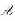在这组基下的矩阵。
判断下列叙述正确与否。
①用P、v操作可以解决互斥与同步问题。
②只要同一信号量上的P、v操作成对地出现，就可以防止引起死锁。
③进程之间因为竞争资源可能会引起死锁。死锁的检测与修复以及死锁的避免策略是对付死锁的主要办法。但是前一种方法所付出的代价要更大。
④在一个单处理机中，最多只能允许有两个进程处于运行状态。
⑤批处理系统不允许用户随时干预自己程序的运行。
⑥如果一个进程正在等待使用处理机，同时除CPU以外其他运行条件已满足，则称该进程为就绪状态。
⑦资源的静态分配就是作业需要的所有资源都得到满足后才投入运行，而且在作业生存期间始终为该作业所占有。
⑧虚存就是把一个实存空间变为多个用户内存空间分配给用户作业使用，，使得每个用户作业都感到好像自己独占一个内存。
⑨为提高计算机处理器和外部设备的利用率，把多个程序同时放入主存储器内，使处理器和外部设备能并行执行，从而提高资源利用率。这种方法称为多道程序设计。
⑩分时系统一定是多道系统，多道系统也一定是分时系统。
问题描述:给定一个赋权无向图G=(V,E),每个顶点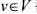
都有权值w(v).如果
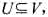,且对任意(u,V)∈E有u∈U或v∈U,就称U为图G的一个顶点覆盖.G的最小权顶点覆盖是指G中所含顶点权之和最小的顶点覆盖.
算法设计:对于给定的无向图G,设计一个优先队列式分支限界法,计算G的最小权顶点覆盖.
数据输入:由文件input.txt给出输入数据.第1行有2个正整数n和m,表示给定的图G有n个顶点和m条边,顶点编号为1,2,...,n.第2行有n个正整数表示n个顶点的权.接下来的m行中,每行有2个正整数u和v,表示图G的一条边(u,v).
结果输出:将计算的最小权顶点覆盖的顶点权值和以及最优解输出到文件output.txt.文件的第1行是最小权顶点覆盖顶点权之和;第2行是最优解xi(1≤i≤n),xi=0表示顶点i不在最小权顶点覆盖中,xi=1表示顶点i在最小权顶点覆盖中.
