题目内容
（请给出正确答案）
[主观题]
证明：设uj是有向网络G中自点1到点j的最短有向路的长度，且对所有的j=2，3，...，n，uj为有
限值，若网络G中的点能编成如下的序号2，3，...，n，使得若i＜j，有ui≤uj且wji≥0，但等号不同时成立或者ui＞uj且wji=+∞，即(j，i)∉A，则方程(6.1)可化简为方程(6.2)。
查看答案
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
如果结果不匹配，请 联系老师 获取答案
更多“证明：设uj是有向网络G中自点1到点j的最短有向路的长度，且…”相关的问题
计算曲线积分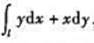
其中
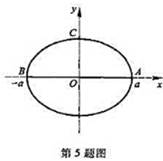
(1)l为自点(a,0)经过上半圆周y=
(a＞0)到点(-a,0);
(2)l为自点(a,0)沿圆周x2+y2=a2的直径到点(-a,0);
(3)l为逆时针方向的圆周x2+y2=a2.
利用动态规划方法求解每对节点之间的最短路径问题(all pairs shortest path problem)时，设有向图 G=＜V,E＞共有n个节点，节点编号1～n，设C是G的成本邻接矩阵，用Dk(I,j)即为图G中节点i到j并且不经过编号比k还大的节点的最短路径的长度(Dn(i,j)即为图G中节点i到j的最短路径长度)，则求解该问题的递推关系式为(62)。
A．Dk(I,j)=Dk-1(I,j)+C(I,j)
B．Dk(I,j)=Dk-1(I,k)+Dk-1(k,j)
C．Dk(I,j)=min{Dk-1(I,j),Dk-1(I,j)+C(I,j)}
D．Dk(I,j)=min{Dk-1(I,j),Dk-1(I,K)+Dk-1(k,j)}
A．Dk(i,j)=Dk-1(i,j)+C(i,j)
B．Dk(i,j)=min{Dk-1(i,j),Dk-1(i,j)+C(i,j)}
C．Dk(i,j)=Dk-1(i,k)+Dk-1(k,j)
D．Dk(i,j)=min{Dk-1(i,j),Dk-1(i,k)+Dk-1(k,j)}
阅读下列函数说明和C函数，将应填入(n)处的字句写在对应栏内。
[说明]
Kruskal算法是一种构造图的最小生成树的方法。设G为一无向连通图，令T是由G的顶点构成的于图，Kmskal算法的基本思想是为T添加适当的边使之成为最小生成树：初始时，T中的点互相不连通；考察G的边集E中的每条边，若它的两个顶点在T中不连通，则将此边添加到T中，同时合并其两顶点所在的连通分量，如此下去，当添加了n-1条边时，T的连通分量个数为1，T便是G的一棵最小生成树。
下面的函数void Kruskal(EdgeType edges[],int n)利用Kruskal算法，构造了有n个顶点的图 edges的最小生成树。其中数组father[]用于记录T中顶点的连通性质：其初值为father[i]=-1 (i=0,1,…,n-1)，表示各个顶点在不同的连通分量上；若有father[i]=j，j＞-1，则顶点i，j连通；函数int Find(int father[],int v)用于返回顶点v所在树形连通分支的根结点。
[函数]
define MAXEDGE 1000
typedef struct
{ int v1;
int v2;
}EdgeType;
void Kruskal(EdgeType edges[],int n)
{ int father[MAXEDGE];
int i,j,vf1,vt2;
for(i=0;i＜n;i+ +) father[i]=-1;
i=0;
j=0;
while(i＜MAXEDGE && j＜(1))
{ vf1=Find(father,edges[i].v1);
vf2=Find(father,edges[i].v2);
if((2))
{(3)=vf1;
(4);
printf("%3d%3d\n",edges[i].v1,edges[i].v2);
}
(5);
}
}
int Find(int father[],int v)
{ int t;
t=v;
while(father[t]＞=0) t=father[t];
return(t);
}
1)设f(x)及G(x)是P[x]中m次及≤m+1次多项式。证明：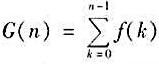
对所有n≥1成立的充分必要条件是G(x+1)-G(x)=f(x)且G(0)=0;
2)证明：对P[x]中任何m次多项式f(x)，必有P[x]中次数≤m+1的多项式G(x)满足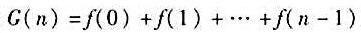
对任何n≥1的整数成立;
3)求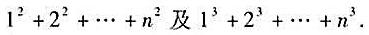
A.N
B.E
C.2E
D.N+E
(60)
A．N
B．E
C．2E
D．N+E
设数域P上nxn矩阵F的特征多项式为f(x)，并设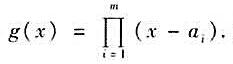
证明：
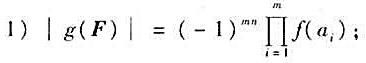
2)对数域P上次数≥1的多项式G(x)有(G(x)，f(x))=1当且仅当|G(F)|≠0。
计算曲线积分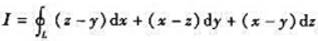
,其中
(I)L是曲线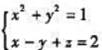
方向是从0z轴正方向往负方向看去为顺时针方向;
(II)L是自点A(1,0,0)经过点B(0,2,0)和点C(0,0,3),又回到点A的三角形围线.
证明定理17.18.
定理17.18:设G*是具有h(k≥2)个连通分支的平面图G的对偶图,n*m*,r*和n,m,r分别为G*和G的顶点数,边数,面数,则
(1)n*=r,(2)m*= m;(3)r*=n-k+1;
(4)设G*的顶点vt*，位于G的面Rt中,则dG*(vt*)=dcg(Rt).
