题目内容
（请给出正确答案）
已知某种白炽灯泡的使用寿命服从正态分布，在某星期中所生产的该种灯泡中随机抽取10只，测得其寿命(单位：h)如下：1067，919，1196，785，1126，936，918，1156，920，948． 试用数字特征法求出寿命总体的均值μ和方差σ2的估计值，并求这种灯泡的寿命大于1300h的概率．
如果结果不匹配，请 联系老师 获取答案
更多“已知某种白炽灯泡的使用寿命服从正态分布，在某星期中所生产的该…”相关的问题
元件寿命的样本均值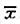
=1920(h)，样本标准差s=150(h)，检验这批元件是否合格(取α=0.01)。
取10件,测得质量(g)如下:
54.0 55.1 53.8 54.2 52.1 54.2 55.0 55.8 55.1 55.3.
如果标准差不变,该生产的零件质量的均值是否有显著差异？(取显著性水平a=0.05).
灯泡厂用4种不同的材料制成灯丝:检验灯线材料这一因素对灯泡寿命的影响若灯泡寿命服从正态分布:不同材料的灯丝制成的灯泡寿命的方差相同，试根据表中试验结果记录，在显著性水平0.05下检验灯泡寿命是否因灯丝材料不同而有显著差异。
为比较A牌和B牌灯泡的寿命，随机抽取A牌灯泡10只，测得平均寿命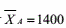
小时，样本标准差S1=52小时，随机抽取B牌灯泡8只，测得平均寿命
小时，样本标准差S2=64小时，设两总体都服从正态分布，且方差相等，求两总体均值差μA-μB的95%置信区间。
已知总体服从正态分布，现抽取一小样本，拟对总体方差进行双侧假设检验，α＝0．05，则原假设的拒绝区域为( )。
利用下面的信息，构建总体均值u的置信区间。 （1）总体服从正态分布，已知σ=500，n=15，x ̄=8900，置信水平为95%； （2）总体不服从正态分布，已知σ=500，n=35，x ̄=8900，置信水平为95%； （3）总体不服从正态分布，σ未知，n=35，x ̄=8900，s=500，置信水平为90%； （4）总体不服从正态分布，σ未知，n=35，x ̄=8900，s=500，置信水平为99%。
设某种清漆的9个样品，其干燥时间(以h计)分别为
6.0 5.7 5.8 6.5 7.0 6.3 5.6 6.1 5.0
设干燥时间总体服从正态分布N(μ，σ2)．求μ的置信水平为0.95的置信区间．
